A DNA sequence motif represented as a sequence logo for the LexA-binding motif.

In biology, a sequence motif is a nucleotide or amino-acid sequence pattern that is widespread and usually assumed to be related to biological function of the macromolecule. For example, an N-glycosylation site motif can be defined as Asn, followed by anything but Pro, followed by either Ser or Thr, followed by anything but Pro residue.

Overview

When a sequence motif appears in the exon of a gene, it may encode the "structural motif" of a protein; that is a stereotypical element of the overall structure of the protein. Nevertheless, motifs need not be associated with a distinctive secondary structure. "Noncoding" sequences are not translated into proteins, and nucleic acids with such motifs need not deviate from the typical shape (e.g. the "B-form" DNA double helix).

Outside of gene exons, there exist regulatory sequence motifs and motifs within the "junk", such as satellite DNA. Some of these are believed to affect the shape of nucleic acids[1] (see for example RNA self-splicing), but this is only sometimes the case. For example, many DNA binding proteins that have affinity for specific DNA binding sites bind DNA in only its double-helical form. They are able to recognize motifs through contact with the double helix's major or minor groove.

Short coding motifs, which appear to lack secondary structure, include those that label proteins for delivery to particular parts of a cell, or mark them for phosphorylation.

Within a sequence or database of sequences, researchers search and find motifs using computer-based techniques of sequence analysis, such as BLAST. Such techniques belong to the discipline of bioinformatics. See also consensus sequence.

Motif Representation

Consider the N-glycosylation site motif mentioned above:

Asn, followed by anything but Pro, followed by either Ser or Thr, followed by anything but Pro

This pattern may be written as N{P}[ST]{P} where N = Asn, P = Pro, S = Ser, T = Thr; {X} means any amino acid except X; and [XY] means either X or Y.

The notation [XY] does not give any indication of the probability of X or Y occurring in the pattern. Observed probabilities can be graphically represented using sequence logos. Sometimes patterns are defined in terms of a probabilistic model such as a hidden Markov model.

Motifs and consensus sequences

The notation [XYZ] means X or Y or Z, but does not indicate the likelihood of any particular match. For this reason, two or more patterns are often associated with a single motif: the defining pattern, and various typical patterns.

For example, the defining sequence for the IQ motif may be taken to be:

[FILV]Qxxx[RK]Gxxx[RK]xx[FILVWY]

where x signifies any amino acid, and the square brackets indicate an alternative (see below for further details about notation).

Usually, however, the first letter is I, and both [RK] choices resolve to R. Since the last choice is so wide, the pattern IQxxxRGxxxR is sometimes equated with the IQ motif itself, but a more accurate description would be a consensus sequence for the IQ motif.

Pattern description notations

Several notations for describing motifs are in use but most of them are variants of standard notations for regular expressions and use these conventions:

  • there is an alphabet of single characters, each denoting a specific amino acid or a set of amino acids;
  • a string of characters drawn from the alphabet denotes a sequence of the corresponding amino acids;
  • any string of characters drawn from the alphabet enclosed in square brackets matches any one of the corresponding amino acids; e.g. [abc] matches any of the amino acids represented by a or b or c.

The fundamental idea behind all these notations is the matching principle, which assigns a meaning to a sequence of elements of the pattern notation:

a sequence of elements of the pattern notation matches a sequence of amino acids if and only if the latter sequence can be partitioned into subsequences in such a way that each pattern element matches the corresponding subsequence in turn.

Thus the pattern [AB] [CDE] F matches the six amino acid sequences corresponding to ACF, ADF, AEF, BCF, BDF, and BEF.

Different pattern description notations have other ways of forming pattern elements. One of these notations is the PROSITE notation, described in the following subsection.

PROSITE pattern notation

The PROSITE notation uses the IUPAC one-letter codes and conforms to the above description with the exception that a concatenation symbol, '-', is used between pattern elements, but it is often dropped between letters of the pattern alphabet.

PROSITE allows the following pattern elements in addition to those described previously:

  • The lower case letter 'x' can be used as a pattern element to denote any amino acid.
  • A string of characters drawn from the alphabet and enclosed in braces (curly brackets) denotes any amino acid except for those in the string. For example, {ST} denotes any amino acid other than S or T.
  • If a pattern is restricted to the N-terminal of a sequence, the pattern is prefixed with '<'.
  • If a pattern is restricted to the C-terminal of a sequence, the pattern is suffixed with '>'.
  • The character '>' can also occur inside a terminating square bracket pattern, so that S[T>] matches both "ST" and "S>".
  • If e is a pattern element, and m and n are two decimal integers with m <= n, then:
    • e(m) is equivalent to the repetition of e exactly m times;
    • e(m,n) is equivalent to the repetition of e exactly k times for any integer k satisfying: m <= k <= n.

Some examples:

  • x(3) is equivalent to x-x-x.
  • x(2,4) matches any sequence that matches x-x or x-x-x or x-x-x-x.

The signature of the C2H2-type zinc finger domain is:

  • C-x(2,4)-C-x(3)-[LIVMFYWC]-x(8)-H-x(3,5)-H

Matrices

A matrix of numbers containing scores for each residue or nucleotide at each position of a fixed-length motif. There are two types of weight matrices.

  • A position frequency matrix (PFM) records the position-dependent frequency of each residue or nucleotide. PFMs can be experimentally determined from SELEX experiments or computationally discovered by tools such as MEME using hidden Markov models.
  • A position weight matrix (PWM) contains log odds weights for computing a match score. A cutoff is needed to specify whether an input sequence matches the motif or not. PWMs are calculated from PFMs. PWMs are also known as PSSMs.

An example of a PFM from the TRANSFAC database for the transcription factor AP-1:

PosACGTIUPAC
016281R
023590S
0300017T
0400170G
0517000A
0601601C
073239T
084724N
099611M
104373N
116317W

The first column specifies the position, the second column contains the number of occurrences of A at that position, the third column contains the number of occurrences of C at that position, the fourth column contains the number of occurrences of G at that position, the fifth column contains the number of occurrences of T at that position, and the last column contains the IUPAC notation for that position. Note that the sums of occurrences for A, C, G, and T for each row should be equal because the PFM is derived from aggregating several consensus sequences.

Motif Discovery

Overview

The sequence motif discovery process has been well-developed since the 1990s. In particular, most of the existing motif discovery research focuses on DNA motifs. With the advances in high-throughput sequencing, such motif discovery problems are challenged by both the sequence pattern degeneracy issues and the data-intensive computational scalability issues.

Process of discovery

A flowchart depicting the process of motif discovery

Motif discovery happens in three major phases. A pre-processing stage where sequences are meticulously prepared in assembly and cleaning steps. Assembly involves selecting sequences that contain the desired motif in large quantities, and extraction of unwanted sequences using clustering. Cleaning then ensures the removal of any confounding elements. Next there is the discovery stage. In this phase sequences are represented using consensus strings or Position-specific Weight Matrices (PWM). After motif representation, an objective function is chosen and a suitable search algorithm is applied to uncover the motifs. Finally the post-processing stage involves evaluating the discovered motifs.[2]

De novo motif discovery

There are software programs which, given multiple input sequences, attempt to identify one or more candidate motifs. One example is the Multiple EM for Motif Elicitation (MEME) algorithm, which generates statistical information for each candidate.[3] There are more than 100 publications detailing motif discovery algorithms; Weirauch et al. evaluated many related algorithms in a 2013 benchmark.[4] The planted motif search is another motif discovery method that is based on combinatorial approach.

Phylogenetic motif discovery

Motifs have also been discovered by taking a phylogenetic approach and studying similar genes in different species. For example, by aligning the amino acid sequences specified by the GCM (glial cells missing) gene in man, mouse and D. melanogaster, Akiyama and others discovered a pattern which they called the GCM motif in 1996.[5] It spans about 150 amino acid residues, and begins as follows:

WDIND*.*P..*...D.F.*W***.**.IYS**...A.*H*S*WAMRNTNNHN

Here each . signifies a single amino acid or a gap, and each * indicates one member of a closely related family of amino acids. The authors were able to show that the motif has DNA binding activity.

A similar approach is commonly used by modern protein domain databases such as Pfam: human curators would select a pool of sequences known to be related and use computer programs to align them and produce the motif profile (Pfam uses HMMs, which can be used to identify other related proteins.[6] A phylogenic approach can also be used to enhance the de novo MEME algorithm, with PhyloGibbs being an example.[7]

De novo motif pair discovery

In 2017, MotifHyades has been developed as a motif discovery tool that can be directly applied to paired sequences.[8]

De novo motif recognition from protein

In 2018, a Markov random field approach has been proposed to infer DNA motifs from DNA-binding domains of proteins.[9]

Motif Discovery Algorithms

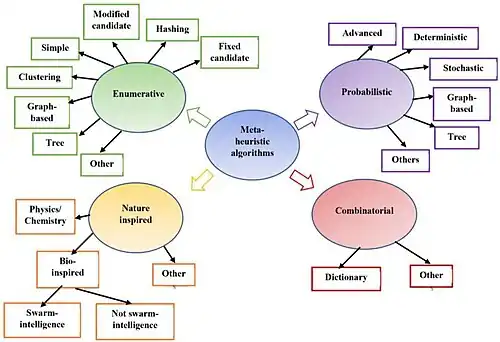
Motif discovery algorithms use diverse strategies to uncover patterns in DNA sequences. Integrating enumerative, probabilistic, and nature-inspired approaches, demonstrate their adaptability, with the use of multiple methods proving effective in enhancing identification accuracy.

Enumerative Approach:[2]

Initiating the motif discovery journey, the enumerative approach witnesses algorithms meticulously generating and evaluating potential motifs. Pioneering this domain are Simple Word Enumeration techniques, such as YMF and DREME, which systematically go through the sequence in search of short motifs. Complementing these, Clustering-Based Methods such as CisFinder employ nucleotide substitution matrices for motif clustering, effectively mitigating redundancy. Concurrently, Tree-Based Methods like Weeder and FMotif exploit tree structures, and Graph Theoretic-Based Methods (e.g., WINNOWER) employ graph representations, demonstrating the richness of enumeration strategies.

Probabilistic Approach:[2]

Diverging into the probabilistic realm, this approach capitalizes on probability models to discern motifs within sequences. MEME, a deterministic exemplar, employs Expectation-Maximization for optimizing Position Weight Matrices (PWMs) and unraveling conserved regions in unaligned DNA sequences. Contrasting this, stochastic methodologies like Gibbs Sampling initiate motif discovery with random motif position assignments, iteratively refining the predictions. This probabilistic framework adeptly captures the inherent uncertainty associated with motif discovery.

Advanced Approach:[2]

Evolving further, advanced motif discovery embraces sophisticated techniques, with Bayesian modeling[10] taking center stage. LOGOS and BaMM, exemplifying this cohort, intricately weave Bayesian approaches and Markov models into their fabric for motif identification. The incorporation of Bayesian clustering methods enhances the probabilistic foundation, providing a holistic framework for pattern recognition in DNA sequences.

Nature-Inspired and Heuristic Algorithms:[2]

A distinct category unfolds, wherein algorithms draw inspiration from the biological realm. Genetic Algorithms (GA), epitomized by FMGA and MDGA,[11] navigate motif search through genetic operators and specialized strategies. Harnessing swarm intelligence principles, Particle Swarm Optimization (PSO), Artificial Bee Colony (ABC) algorithms, and Cuckoo Search (CS) algorithms, featured in GAEM, GARP, and MACS, venture into pheromone-based exploration. These algorithms, mirroring nature's adaptability and cooperative dynamics, serve as avant-garde strategies for motif identification. The synthesis of heuristic techniques in hybrid approaches underscores the adaptability of these algorithms in the intricate domain of motif discovery.

This chart shows many different types of algorithms used in the discovery of sequence motifs and their categories

Motif Cases

Three-dimensional chain codes

The E. coli lactose operon repressor LacI (PDB: 1lcc​ chain A) and E. coli catabolite gene activator (PDB: 3gap​ chain A) both have a helix-turn-helix motif, but their amino acid sequences do not show much similarity, as shown in the table below. In 1997, Matsuda, et al. devised a code they called the "three-dimensional chain code" for representing the protein structure as a string of letters. This encoding scheme reveals the similarity between the proteins much more clearly than the amino acid sequence (example from article):[12] The code encodes the torsion angles between alpha-carbons of the protein backbone. "W" always corresponds to an alpha helix.

3D chain codeAmino acid sequence
1lccA TWWWWWWWKCLKWWWWWWGLYDVAEYAGVSYQTVSRVV
3gapA KWWWWWWGKCFKWWWWWWWRQEIGQIVGCSRETVGRIL

See also

References

Primary sources

  1. ↑ Dlakić, Mensur; Harrington, Rodney E. (1996). "The Effects of Sequence Context on DNA Curvature". Proceedings of the National Academy of Sciences of the United States of America. 93 (9): 3847–3852. Bibcode:1996PNAS...93.3847D. doi:10.1073/pnas.93.9.3847. ISSN 0027-8424. JSTOR 39155. PMC 39447. PMID 8632978.
  2. 1 2 3 4 5 Hashim, Fatma A.; Mabrouk, Mai S.; Al-Atabany, Walid (2019). "Review of Different Sequence Motif Finding Algorithms". Avicenna Journal of Medical Biotechnology. 11 (2): 130–148. ISSN 2008-2835. PMC 6490410. PMID 31057715.
  3. ↑ Bailey TL, Williams N, Misleh C, Li WW (July 2006). "MEME: discovering and analyzing DNA and protein sequence motifs". Nucleic Acids Research. 34 (Web Server issue): W369-73. doi:10.1093/nar/gkl198. PMC 1538909. PMID 16845028.
  4. ↑ Weirauch MT, Cote A, Norel R, Annala M, Zhao Y, Riley TR, et al. (February 2013). "Evaluation of methods for modeling transcription factor sequence specificity". Nature Biotechnology. 31 (2): 126–34. doi:10.1038/nbt.2486. PMC 3687085. PMID 23354101.
  5. ↑ Akiyama Y, Hosoya T, Poole AM, Hotta Y (December 1996). "The gcm-motif: a novel DNA-binding motif conserved in Drosophila and mammals". Proceedings of the National Academy of Sciences of the United States of America. 93 (25): 14912–6. Bibcode:1996PNAS...9314912A. doi:10.1073/pnas.93.25.14912. PMC 26236. PMID 8962155.
  6. ↑ "Modelling in Pfam". Pfam. Retrieved 14 December 2023.
  7. ↑ Siddharthan R, Siggia ED, van Nimwegen E (December 2005). "PhyloGibbs: a Gibbs sampling motif finder that incorporates phylogeny". PLOS Computational Biology. 1 (7): e67. Bibcode:2005PLSCB...1...67S. doi:10.1371/journal.pcbi.0010067. PMC 1309704. PMID 16477324.
  8. ↑ Wong KC (October 2017). "MotifHyades: expectation maximization for de novo DNA motif pair discovery on paired sequences". Bioinformatics. 33 (19): 3028–3035. doi:10.1093/bioinformatics/btx381. PMID 28633280.
  9. ↑ Wong KC (September 2018). "DNA Motif Recognition Modeling from Protein Sequences". iScience. 7: 198–211. Bibcode:2018iSci....7..198W. doi:10.1016/j.isci.2018.09.003. PMC 6153143. PMID 30267681.
  10. ↑ Miller, Andrew K.; Print, Cristin G.; Nielsen, Poul M. F.; Crampin, Edmund J. (2010-11-18). "A Bayesian search for transcriptional motifs". PLOS ONE. 5 (11): e13897. Bibcode:2010PLoSO...513897M. doi:10.1371/journal.pone.0013897. ISSN 1932-6203. PMC 2987817. PMID 21124986.
  11. ↑ Che, Dongsheng; Song, Yinglei; Rasheed, Khaled (2005-06-25). "MDGA: Motif discovery using a genetic algorithm". Proceedings of the 7th annual conference on Genetic and evolutionary computation. GECCO '05. New York, NY, USA: Association for Computing Machinery. pp. 447–452. doi:10.1145/1068009.1068080. ISBN 978-1-59593-010-1. S2CID 7892935.
  12. ↑ Matsuda H, Taniguchi F, Hashimoto A (1997). "An approach to detection of protein structural motifs using an encoding scheme of backbone conformations" (PDF). Pacific Symposium on Biocomputing. Pacific Symposium on Biocomputing: 280–91. PMID 9390299.

Further reading

Primary sources

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.