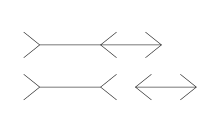
Two sets of arrows that exhibit the Müller-Lyer optical illusion. The set on the bottom represents the classic Müller-Lyer stimulus, while on the top is its Brentano modification. All the shafts of the arrows are of the same physical length.

The Müller-Lyer illusion is an optical illusion consisting of three stylized arrows. When viewers are asked to place a mark on the figure at the midpoint, they tend to place it more towards the "tail" end. The illusion was devised by Franz Carl Müller-Lyer (1857–1916), a German sociologist, in 1889.[1][2][3]

A variation of the same effect (and the most common form in which it is seen today) consists of a set of arrow-like figures. Straight line segments of equal length comprise the "shafts" of the arrows, while shorter line segments (called the fins) protrude from the ends of the shaft. The fins can point inwards to form an arrow "head" or outwards to form an arrow "tail". The line segment forming the shaft of the arrow with two tails is perceived to be longer than that forming the shaft of the arrow with two heads.

Variation in perception

Research has shown that sensation of the Müller-Lyer illusion can vary. Around the turn of the 20th century, W. H. R. Rivers noted that indigenous people of the Australian Murray Island were less susceptible to the Müller-Lyer illusion than were Europeans.[4] Rivers suggested that this difference may be because Europeans live in more rectilinear environments than the islanders.[5] Similar results were also observed by John W. Berry in his work on Inuit, urban Scots, and the Temne people in the 1960s.[6]

In 1963, Segall, Campbell and Herskovitz compared susceptibility to four different visual illusions in three population samples of Caucasians, twelve of Africans, and one from the Philippines. For the Müller-Lyer illusion, the mean fractional misperception of the length of the line segments varied from 1.4% to 20.3%. The three European-derived samples were the three most susceptible samples, while the San foragers of the Kalahari desert were the least susceptible.[7]

In 1965, following a debate between Donald T. Campbell and Melville J. Herskovits on whether culture can influence such basic aspects of perception such as the length of a line, they suggested that their student Marshall Segall investigate the problem. In their definitive paper of 1966, they investigated seventeen cultures and showed that people in different cultures differ substantially on how they experience the Müller-Lyer stimuli. They wrote that "European and American city dwellers have a much higher percentage of rectangularity in their environments than non-Europeans and so are more susceptible to that illusion."[8]

They also used the word "carpentered" for the environments that Europeans mostly live in - characterized by straight lines, right angles, and square corners.

These conclusions were challenged in later work by Gustav Jahoda, who compared members of an African tribe living in a traditional rural environment with members of same group living in African cities. Here, no significant difference in susceptibility to the M-L illusion was found. Subsequent work by Jahoda suggested that retinal pigmentation may have a role in the differing perceptions on this illusion,[9] and this was verified later by Pollack (1970). It is believed now that not "carpenteredness", but the density of pigmentation in the eye is related to susceptibility to the M-L illusion. Dark-skinned people often have denser eye pigmentation.[10]

A later study was conducted in 1978 by Ahluwalia on children and young adults from Zambia. Subjects from rural areas were compared with subjects from urban areas. The subjects from urban areas were shown to be considerably more susceptible to the illusion, as were younger subjects.[11] While this by no means confirms the carpentered world hypothesis as such, it provides evidence that differences in the environment can create differences in the perception of the Müller-Lyer illusion, even within a given culture. Experiments have been reported suggesting that pigeons perceive the standard Müller-Lyer illusion, but not the reversed.[12] Experiments on parrots have also been reported with similar results.[13]

Perspective explanation

The Müller-Lyer effect in a non-illusion

One possible explanation, given by Richard Gregory,[14] is that the Müller-Lyer illusion occurs because the visual system learns that the "angles in" configuration corresponds to an rectilinear object, such as the convex corner of a room, which is closer, and the "angles out" configuration corresponds to an object which is far away, such as the concave corner of a room. However, in a recent report[15] Catherine Howe and Dale Purves contradicted Gregory's explanation:

Although Gregory's intuition about the empirical significance of the Müller-Lyer stimulus points in the right general direction (i.e., an explanation based on past experience with the sources of such stimuli), convex and concave corners contribute little if anything to the Müller-Lyer effect.

Neural nets in the visual system of human beings learn how to make a very efficient interpretation of 3D scenes. That is why when somebody goes away from us, we do not perceive them as getting shorter. And when we stretch one arm and look at the two hands we do not perceive one hand smaller than the other. Visual illusions are sometimes held to show us that what we see is an image created in our brain. Our brain supposedly projects the image of the smaller hand to its correct distance in our internal 3D model. This is what is called the size constancy mechanism hypothesis.

In the Müller-Lyer illusion, the visual system would in this explanation detect the depth cues, which are usually associated with 3D scenes, and incorrectly decide it is a 3D drawing. Then the size constancy mechanism would make us see an erroneous length of the object which, for a true perspective drawing, would be farther away.

In the perspective drawing in the figure, we see that in usual scenes the heuristic works quite well. The width of the rug should obviously be considered shorter than the length of the wall in the back.

Centroid explanation

The classic Müller-Lyer figures (A) and three modifications (having no shaft line) of the Brentano versions of illusory figures comprising different contextual flanks: separate dots (B), the Müller-Lyer wings (C), and arcs of a circle (D, distances between the points seem to be different)
A dynamic visual demonstration by Italian researcher Gianni A. Sarcone: the blue and black segments of the star are equal in length and always the same length, though they appear to alternately stretch and shrink.
This variant of dynamic Müller-Lyer illusion by Italian researcher Gianni A. Sarcone shows that though the collinear blue and red segments seem to oscillate up and down, they are always the same length. Nothing moves except the arrows at the endpoints of each color segments. This visual illusion also involves a dynamic "neon color spreading" effect.

According to the so-called centroid hypothesis, judgments of distance between visual objects are strongly affected by the neural computation of the centroids of the luminance profiles of the objects, in that the position of the centroid of an image determines its perceived location.[16] Morgan et al., suggest that the visual procedure of centroid extraction is causally related to a spatial pooling of the positional signals evoked by the neighboring object parts.[17] Though the integration coarsens the positional acuity, such pooling seems to be quite biologically substantiated since it allows fast and reliable assessment of the location of the visual object as whole, irrespective of its size, the shape complexity, and illumination conditions. Concerning the Müller-Lyer and similar illusions, the pattern of neural excitation evoked by contextual flank (e.g., the Müller-Lyer wings themselves) overlaps with that caused by the stimulus terminator (e.g., the wings apex), thereby leading (due to the shift of the centroid of summed excitation) to its perceptual displacement. The crucial point in the centroid explanation regarding the positional shifts of the stimulus terminators in the direction of the centroids of contextual flanks was confirmed in psychophysical examination of illusory figures with rotating distractors.[18] The relative displacement of all stimulus terminators leads to misjudgment of distances between them; that is, the illusion occurs as a side effect due to necessarily low spatial resolution of the neural mechanism of assessment of the relative location of the visual objects. Besides, it was shown [19] that well-known asymmetry in manifestation of the wings-in and wings-out modifications of the Müller-Lyer illusion can be successfully explained by supplemental effects of the filled-space illusion.

Brentano figure with the rotating Müller-Lyer wings (distractors); actually, apices of the wings (stimulus terminators) are aligned and spaced equidistantly

References

  1. ↑ Müller-Lyer, FC (1889). "Optische Urteilstäuschungen". Archiv für Physiologie Suppl. 1889: 263–270.
  2. ↑ Brentano, F (1892). "Über ein optisches Paradoxon". Zeitschrift für Psychologie. 3: 349–358.
  3. ↑ Müller-Lyer, FC (1894). "Über Kontrast und Konfluxion". Zeitschrift für Psychologie. 9: 1–16.
  4. ↑ Rivers 1901: The measurement of visual illusion Rep. Brit. Ass., p. 818
  5. ↑ Rivers, W. H. R. (1901). Vision. In A. C. Haddon (Ed.), Reports of the Cambridge Anthropological Expedition to Torres Straits (pp. 1– 132). Cambridge, UK: Cambridge University Press.
  6. ↑ Berry, John W. (1968), "Ecology, perceptual development and the Müller-Lyer illusion", British Journal of Psychology, 59 (3): 205–210, doi:10.1111/j.2044-8295.1968.tb01134.x, PMID 5760069
  7. ↑ Cultural Differences in the Perception of Geometric Illusions Author(s): Marshall H. Segall, Donald T. Campbell, Melville J. Herskovits Source: Science, New Series, Vol. 139, No. 3556 (February 22, 1963), pp. 769-771
  8. ↑ "APA PsycNet".
  9. ↑ Jahoda, Gustav (1971). "Retinal pigmentation, illusion susceptibility and space perception". International Journal of Psychology. 6 (3): 199–207. doi:10.1080/00207597108246683.
  10. ↑ Cole, Michael; Barbara Means; Comparative Studies of How People Think: An Introduction, 1986. Fatima.S & Kanwal.A
  11. ↑ An intra-cultural investigation of susceptibility to "perspective" and "non-perspective" spatial illusions, Br. J. Psychol., 1978, 69, 233-241
  12. ↑ Nakamura, Noriyuki; et al. (2006). "Perception of the Standard and the Reversed Müller-Lyer Figures in Pigeons (Columba livia) and Humans (Homo sapiens)". Journal of Comparative Psychology. Journal of Comparative Psychology. 2006 August Vol 120(3) 252-261. 120 (3): 252–261. doi:10.1037/0735-7036.120.3.252. PMID 16893262.
  13. ↑ Pepperberg, Irene; et al. "The Müller-Lyer illusion is processed by a Grey Parrot (Psittacus erithacus)" (PDF). Perception 37:765-781. Archived from the original (PDF) on 2013-05-08. Retrieved 2011-07-30.
  14. ↑ Richard L. Gregory, Eye and Brain, McGraw Hill, 1966.
  15. ↑ The Müller-Lyer illusion explained by the statistics of image–source relationships Catherine Q. Howe and Dale Purves* PNAS January 25, 2005 vol. 102 no. 4 1234-1239
  16. ↑ Whitaker, D., McGraw, P. V., Pacey, I., Barrett, B. T. (1996). Centroid analysis predicts visual localization of first- and second-order stimuli. Vision Research, 36, 2957-2970.
  17. ↑ Morgan M.J., Hole G.J., & Glennerster A. (1990). Biases and sensitivities in geometrical illusions. Vision Research, 30, 1793−1810.
  18. ↑ Bulatov A., Bertulis A., Mickienė L., Surkys T., Bielevičius A. (2011) Contextual flanks' tilting and magnitude of illusion of extent. Vision Research 51(1), 58−64. https://doi.org/10.1016/j.visres.2010.09.033
  19. ↑ Bulatov A., Bulatova N., Marma V., Kučinskas L. (2022) Quantitative study of asymmetry in the manifestation of the wings-in and wings-out versions of the Müller-Lyer illusion. Attention, Perception, & Psychophysics, 84, 560−575. https://doi.org/10.3758/s13414-021-02412-z
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.