Carathéodory's theorem is a theorem in convex geometry. It states that if a point lies in the convex hull of a set , then can be written as the convex combination of at most points in . More sharply, can be written as the convex combination of at most extremal points in , as non-extremal points can be removed from without changing the membership of in the convex hull.
Its equivalent theorem for conical combinations states that if a point lies in the conical hull of a set , then can be written as the conical combination of at most points in .[1]: 257
The similar theorems of Helly and Radon are closely related to Carathéodory's theorem: the latter theorem can be used to prove the former theorems and vice versa.[2]
The result is named for Constantin Carathéodory, who proved the theorem in 1911 for the case when is compact.[3] In 1914 Ernst Steinitz expanded Carathéodory's theorem for arbitrary set.[4]
Example
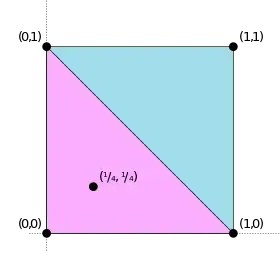
Carathéodory's theorem in 2 dimensions states that we can construct a triangle consisting of points from P that encloses any point in the convex hull of P.
For example, let P = {(0,0), (0,1), (1,0), (1,1)}. The convex hull of this set is a square. Let x = (1/4, 1/4) in the convex hull of P. We can then construct a set {(0,0),(0,1),(1,0)} = P′, the convex hull of which is a triangle and encloses x.
Proof
Note: We will only use the fact that is an ordered field, so the theorem and proof works even when is replaced by any field , together with a total order.
We first formally state Carathéodory's theorem:[5]
Carathéodory's theorem — If , then is the nonnegative sum of at most points of .
If , then is the convex sum of at most points of .
The essence of Carathéodory's theorem is in the finite case. This reduction to the finite case is possible because is the set of finite convex combination of elements of (see the convex hull page for details).
Lemma — If then , exists such that , and at most of them are nonzero.
With the lemma, Carathéodory's theorem is a simple extension:
For any , represent for some , then , and we use the lemma.
The second part reduces to the first part by "lifting up one dimension", a common trick used to reduce affine geometry to linear algebra, and reduce convex bodies to convex cones.
Explicitly, let , then identify with the subset . This induces an embedding of into .
Any , by first part, has a "lifted" representation where at most of are nonzero. That is, , and , which completes the proof.
This is trivial when . If we can prove it for all , then by induction we have proved it for all . Thus it remains to prove it for . This we prove by induction on .
Base case: , trivial.
Induction case. Represent . If some , then the proof is finished. So assume all
If is linearly dependent, then we can use induction on its linear span to eliminate one nonzero term in , and thus eliminate it in as well.
Else, there exists , such that . Then we can interpolate a full interval of representations:
If for all , then set . Otherwise, let be the smallest such that one of . Then we obtain a convex representation of with nonzero terms.
Alternative proofs uses Helly's theorem or the Perron–Frobenius theorem.[6][7]
Variants
Carathéodory's number
For any nonempty , define its Carathéodory's number to be the smallest integer , such that for any , there exists a representation of as a convex sum of up to elements in .
Carathéodory's theorem simply states that any nonempty subset of has Carathéodory's number . This upper bound is not necessarily reached. For example, the unit sphere in has Carathéodory's number equal to 2, since any point inside the sphere is the convex sum of two points on the sphere.
With additional assumptions on , upper bounds strictly lower than can be obtained.[8]
Dimensionless variant
Recently, Adiprasito, Barany, Mustafa and Terpai proved a variant of Caratheodory's theorem that does not depend on the dimension of the space.[9]
Colorful Carathéodory theorem
Let X1, ..., Xd+1 be sets in Rd and let x be a point contained in the intersection of the convex hulls of all these d+1 sets.
Then there is a set T = {x1, ..., xd+1}, where x1 ∈ X1, ..., xd+1 ∈ Xd+1, such that the convex hull of T contains the point x.[10]
By viewing the sets X1, ..., Xd+1 as different colors, the set T is made by points of all colors, hence the "colorful" in the theorem's name.[11] The set T is also called a rainbow simplex, since it is a d-dimensional simplex in which each corner has a different color.[12]
This theorem has a variant in which the convex hull is replaced by the conical hull.[10]: Thm.2.2 Let X1, ..., Xd be sets in Rd and let x be a point contained in the intersection of the conical hulls of all these d sets. Then there is a set T = {x1, ..., xd}, where x1 ∈ X1, ..., xd ∈ Xd, such that the conical hull of T contains the point x.[10]
Mustafa and Ray extended this colorful theorem from points to convex bodies.[12]
The computational problem of finding the colorful set lies in the intersection of the complexity classes PPAD and PLS.[13]
See also
Notes
- ↑ Lovász, László; Plummer, M. D. (1986). Matching Theory. Annals of Discrete Mathematics. Vol. 29. North-Holland. ISBN 0-444-87916-1. MR 0859549.
- ↑ Danzer, L.; Grünbaum, B.; Klee, V. (1963). "Helly's theorem and its relatives". Convexity. Proc. Symp. Pure Math. Vol. 7. American Mathematical Society. pp. 101–179. See in particular p.109
- ↑ Carathéodory, C. (1911). "Über den Variabilitätsbereich der Fourier'schen Konstanten von positiven harmonischen Funktionen". Rendiconti del Circolo Matematico di Palermo (1884–1940) (in German). 32 (1): 193–217[see p.200 bottom]. doi:10.1007/BF03014795. S2CID 120032616.
- ↑ Steinitz, Ernst (1913). "Bedingt konvergente Reihen und konvexe Systeme". J. Reine Angew. Math. 1913 (143): 128–175. doi:10.1515/crll.1913.143.128. S2CID 120411668.
- ↑ Leonard, I. Ed; Lewis, J. E. (2016). "3.3 Convex Hulls". Geometry of convex sets. Hoboken, New Jersey: Wiley Blackwell. ISBN 978-1-119-02266-4.
- ↑ Eggleston, H. G. (1958). Convexity. Cambridge University Press. doi:10.1017/cbo9780511566172. ISBN 9780511566172. See pages 40–41.
- ↑ Naszódi, Márton; Polyanskii, Alexandr (2021). "Perron and Frobenius Meet Carathéodory". The Electronic Journal of Combinatorics. 28 (3). arXiv:1901.00540. doi:10.37236/9996. S2CID 119656227.
- ↑ Bárány, Imre; Karasev, Roman (2012-07-20). "Notes About the Carathéodory Number". Discrete & Computational Geometry. 48 (3): 783–792. arXiv:1112.5942. doi:10.1007/s00454-012-9439-z. ISSN 0179-5376. S2CID 9090617.
- ↑ Adiprasito, Karim; Bárány, Imre; Mustafa, Nabil H.; Terpai, Tamás (2019-08-28). "Theorems of Carathéodory, Helly, and Tverberg without dimension". arXiv:1806.08725 [math.MG].
- 1 2 3 Bárány, Imre (1982-01-01). "A generalization of carathéodory's theorem". Discrete Mathematics. 40 (2–3): 141–152. doi:10.1016/0012-365X(82)90115-7. ISSN 0012-365X.
- ↑ Montejano, Luis; Fabila, Ruy; Bracho, Javier; Bárány, Imre; Arocha, Jorge L. (2009-09-01). "Very Colorful Theorems". Discrete & Computational Geometry. 42 (2): 142–154. doi:10.1007/s00454-009-9180-4. ISSN 1432-0444.
- 1 2 Mustafa, Nabil H.; Ray, Saurabh (2016-04-06). "An optimal generalization of the Colorful Carathéodory theorem". Discrete Mathematics. 339 (4): 1300–1305. doi:10.1016/j.disc.2015.11.019. ISSN 0012-365X.
- ↑ Meunier, Frédéric; Mulzer, Wolfgang; Sarrabezolles, Pauline; Stein, Yannik (2017-01-01), "The Rainbow at the End of the Line ? A PPAD Formulation of the Colorful Carathéodory Theorem with Applications", Proceedings of the 2017 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), Proceedings, Society for Industrial and Applied Mathematics, pp. 1342–1351, arXiv:1608.01921, doi:10.1137/1.9781611974782.87, ISBN 978-1-61197-478-2, S2CID 5784949
Further reading
- Eckhoff, J. (1993). "Helly, Radon, and Carathéodory type theorems". Handbook of Convex Geometry. Vol. A, B. Amsterdam: North-Holland. pp. 389–448.
- Mustafa, Nabil; Meunier, Frédéric; Goaoc, Xavier; De Loera, Jesús (2019). "The discrete yet ubiquitous theorems of Carathéodory, Helly, Sperner, Tucker, and Tverberg". Bulletin of the American Mathematical Society. 56 (3): 415–511. arXiv:1706.05975. doi:10.1090/bull/1653. ISSN 0273-0979. S2CID 32071768.
External links
- Concise statement of theorem in terms of convex hulls (at PlanetMath)