One-key MAC (OMAC) is a message authentication code constructed from a block cipher much like the CBC-MAC algorithm.

Officially there are two OMAC algorithms (OMAC1 and OMAC2) which are both essentially the same except for a small tweak. OMAC1 is equivalent to CMAC, which became an NIST recommendation in May 2005.

It is free for all uses: it is not covered by any patents.[1] In cryptography, CMAC is a block cipher-based message authentication code algorithm.[2] It may be used to provide assurance of the authenticity and, hence, the integrity of data. This mode of operation fixes security deficiencies of CBC-MAC (CBC-MAC is secure only for fixed-length messages).

The core of the CMAC algorithm is a variation of CBC-MAC that Black and Rogaway proposed and analyzed under the name XCBC[3] and submitted to NIST.[4] The XCBC algorithm efficiently addresses the security deficiencies of CBC-MAC, but requires three keys. Iwata and Kurosawa proposed an improvement of XCBC and named the resulting algorithm One-Key CBC-MAC (OMAC) in their papers.[5] They later submitted OMAC1,[6] a refinement of OMAC, and additional security analysis.[7] The OMAC algorithm reduces the amount of key material required for XCBC. CMAC is equivalent to OMAC1.

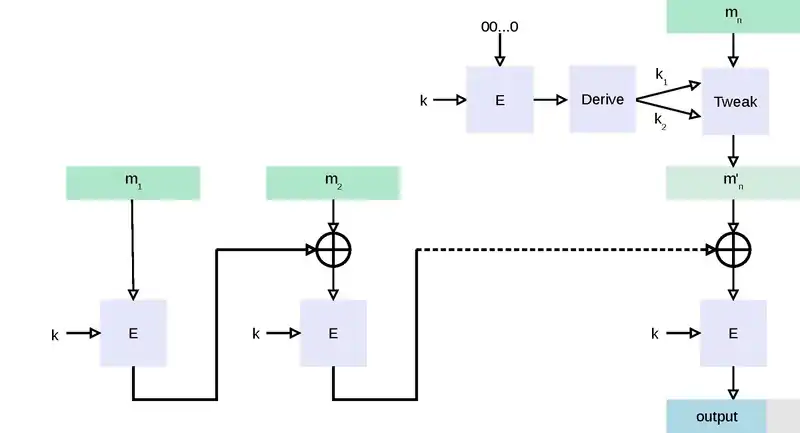
To generate an ℓ-bit CMAC tag (t) of a message (m) using a b-bit block cipher (E) and a secret key (k), one first generates two b-bit sub-keys (k1 and k2) using the following algorithm (this is equivalent to multiplication by x and x2 in a finite field GF(2b)). Let ≪ denote the standard left-shift operator and ⊕ denote bit-wise exclusive or:

  1. Calculate a temporary value k0 = Ek(0).
  2. If msb(k0) = 0, then k1 = k0 ≪ 1, else k1 = (k0 ≪ 1) ⊕ C; where C is a certain constant that depends only on b. (Specifically, C is the non-leading coefficients of the lexicographically first irreducible degree-b binary polynomial with the minimal number of ones: 0x1B for 64-bit, 0x87 for 128-bit, and 0x425 for 256-bit blocks.)
  3. If msb(k1) = 0, then k2 = k1 ≪ 1, else k2 = (k1 ≪ 1) ⊕ C.
  4. Return keys (k1, k2) for the MAC generation process.

As a small example, suppose b = 4, C = 00112, and k0 = Ek(0) = 01012. Then k1 = 10102 and k2 = 0100 ⊕ 0011 = 01112.

The CMAC tag generation process is as follows:

  1. Divide message into b-bit blocks m = m1 ∥ ... ∥ mn−1 ∥ mn, where m1, ..., mn−1 are complete blocks. (The empty message is treated as one incomplete block.)
  2. If mn is a complete block then mn′ = k1 ⊕ mn else mn′ = k2 ⊕ (mn ∥ 10...02).
  3. Let c0 = 00...02.
  4. For i = 1, ..., n − 1, calculate ci = Ek(ci−1 ⊕ mi).
  5. cn = Ek(cn−1 ⊕ mn′)
  6. Output t = msbℓ(cn).

The verification process is as follows:

  1. Use the above algorithm to generate the tag.
  2. Check that the generated tag is equal to the received tag.

Implementations

References

  1. ↑ Rogaway, Phillip. "CMAC: Non-licensing". Retrieved May 27, 2020. Phillip Rogaway's statement on intellectual property status of CMAC
  2. ↑ Dworkin, Morris (2016). "Recommendation for Block Cipher Modes of Operation: The CMAC Mode for Authentication" (PDF). doi:10.6028/nist.sp.800-38b. {{cite journal}}: Cite journal requires |journal= (help)
  3. ↑ Black, John; Rogaway, Phillip (2000-08-20). Advances in Cryptology – CRYPTO 2000. Springer, Berlin, Heidelberg. pp. 197–215. doi:10.1007/3-540-44598-6_12. ISBN 978-3540445982.
  4. ↑ Black, J; Rogaway, P. "A Suggestion for Handling Arbitrary-Length Messages with the CBC MAC" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
  5. ↑ Iwata, Tetsu; Kurosawa, Kaoru (2003-02-24). "OMAC: One-Key CBC MAC". Fast Software Encryption. Lecture Notes in Computer Science. Vol. 2887. Springer, Berlin, Heidelberg. pp. 129–153. doi:10.1007/978-3-540-39887-5_11. ISBN 978-3-540-20449-7.
  6. ↑ Iwata, Tetsu; Kurosawa, Kaoru (2003). "OMAC: One-Key CBC MAC – Addendum" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
  7. ↑ Iwata, Tetsu; Kurosawa, Kaoru (2003-12-08). "Stronger Security Bounds for OMAC, TMAC, and XCBC". In Johansson, Thomas; Maitra, Subhamoy (eds.). Progress in Cryptology - INDOCRYPT 2003. Lecture Notes in Computer Science. Vol. 2904. Springer Berlin Heidelberg. pp. 402–415. CiteSeerX 10.1.1.13.8229. doi:10.1007/978-3-540-24582-7_30. ISBN 9783540206095.
  8. ↑ "Impacket is a collection of Python classes for working with network protocols.: SecureAuthCorp/impacket". 15 December 2018 – via GitHub.
  9. ↑ "Ruby C extension for the AES-CMAC keyed hash function (RFC 4493): louismullie/cmac-rb". 4 May 2016 – via GitHub.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.