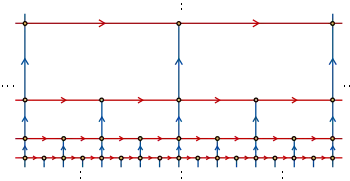

_Cayley_Graph.gif)
In the mathematical field of group theory, the Baumslag–Solitar groups are examples of two-generator one-relator groups that play an important role in combinatorial group theory and geometric group theory as (counter)examples and test-cases. They are given by the group presentation
For each integer m and n, the Baumslag–Solitar group is denoted BS(m, n). The relation in the presentation is called the Baumslag–Solitar relation.
Some of the various BS(m, n) are well-known groups. BS(1, 1) is the free abelian group on two generators, and BS(1, −1) is the fundamental group of the Klein bottle.
The groups were defined by Gilbert Baumslag and Donald Solitar in 1962 to provide examples of non-Hopfian groups. The groups contain residually finite groups, Hopfian groups that are not residually finite, and non-Hopfian groups.
Linear representation
Define
The matrix group G generated by A and B is a homomorphic image of BS(m, n), via the homomorphism induced by
It is worth noting that this will not, in general, be an isomorphism. For instance if BS(m, n) is not residually finite (i.e. if it is not the case that |m| = 1, |n| = 1, or |m| = |n|[1]) it cannot be isomorphic to a finitely generated linear group, which is known to be residually finite by a theorem of Anatoly Maltsev.[2]
See also
Notes
- ↑ See Nonresidually Finite One-Relator Groups by Stephen Meskin for a proof of the residual finiteness condition
- ↑ Anatoliĭ Ivanovich Mal'cev, "On the faithful representation of infinite groups by matrices" Translations of the American Mathematical Society (2), 45 (1965), pp. 1–18
References
- D.J. Collins (2001) [1994], "Baumslag–Solitar group", Encyclopedia of Mathematics, EMS Press
- Gilbert Baumslag and Donald Solitar, Some two-generator one-relator non-Hopfian groups, Bulletin of the American Mathematical Society 68 (1962), 199–201. MR0142635