An electron in a Bohr model atom, moving from quantum level n = 3 to n = 2 and releasing a photon.

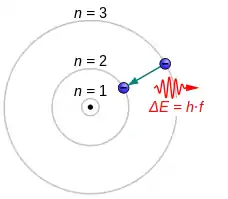
In atomic physics and chemistry, an atomic electron transition (also called an electronic (de-)excitation, atomic transition, or quantum jump) is a change (or jump) of an electron from one energy level to another within an atom^[1] or artificial atom.^[2] It appears discontinuous as the electron "jumps" from one quantized energy level to another, typically in a few nanoseconds or less.

Electron transitions cause the emission or absorption of electromagnetic radiation in the form of quantized units called photons. Their statistics are Poissonian, and the time between jumps is exponentially distributed.^[3] The damping time constant (which ranges from nanoseconds to a few seconds) relates to the natural, pressure, and field broadening of spectral lines. The larger the energy separation of the states between which the electron jumps, the shorter the wavelength of the photon emitted.^[4] The emitted photon changes the kinetic energy of the atom, enabling the laser cooling technology to slow down the motion of atoms.

History

Danish physicist Niels Bohr first theorized that electrons can perform quantum jumps in 1913.^[5] Soon after, James Franck and Gustav Ludwig Hertz proved experimentally that atoms have quantized energy states.^[6]

The observability of quantum jumps was predicted by Hans Dehmelt in 1975, and they were first observed using trapped ions of barium at University of Hamburg and mercury at NIST in 1986.^[4]

Theory

Consider an atom interacting with an oscillating electric field produced by electromagnetic radiation:

${\displaystyle E(t)=|{\textbf {E}}_{0}|Re(e^{-i{\omega }t}{\hat {\textbf {e}}}_{rad})}$

(1)

with amplitude ${\displaystyle |{\textbf {E}}_{0}|}$, angular frequency ${\displaystyle \omega }$, and polarization vector ${\displaystyle {\hat {\textbf {e}}}_{rad}}$.^[7] Note that the actual phase is ${\displaystyle (\omega t-{\textbf {k}}\cdot {\textbf {r}})}$. However, in many cases, the variation of ${\displaystyle {\textbf {k}}\cdot {\textbf {r}}}$ is small over the atom (or equivalently, the radiation wavelength is much greater than the size of an atom) and this term can be ignored. This is called the dipole approximation. The atom can also interact with the oscillating magnetic field produced by the radiation, although much more weakly.

The Hamiltonian for this interaction, analogous to the energy of a classical dipole in a electric field, is ${\displaystyle H_{I}=e{\textbf {r}}\cdot {\textbf {E}}(t)}$. The stimulated transition rate can be calculated using time-dependent perturbation theory; however, the result can be summarized using Fermi's golden rule:

$${\displaystyle Rate\propto |eE_{0}|^{2}\times |\langle 2|{\textbf {r}}\cdot {\hat {\textbf {e}}}_{rad}|1\rangle |^{2}}$$

The dipole matrix element can be decompose into the product of the radial integral and the angular integral. The angular integral is zero unless the selection rules for the atomic transition are satisfied.

Recent discoveries

In 2019, it was demonstrated in an experiment with a superconducting artificial atom consisting of two strongly-hybridized transmon qubits placed inside a readout resonator cavity at 15 mK, that the evolution of some jumps is continuous, coherent, deterministic, and reversible.^[8] On the other hand, other quantum jumps are inherently unpredictable.^[9]

See also

References

External links

Look up quantum leap in Wiktionary, the free dictionary.

• Schrödinger, Erwin (August 1952). "Are there quantum jumps? Part I" (PDF). The British Journal for the Philosophy of Science. 3 (10): 109–123. doi:10.1093/bjps/iii.10.109. Part 2
• "There are no quantum jumps, nor are there particles!" by H. D. Zeh, Physics Letters A172, 189 (1993).
• Ball, Philip (June 5, 2019). "Quantum Leaps, Long Assumed to Be Instantaneous, Take Time". Quanta Magazine. Retrieved June 6, 2019.
• "Surface plasmon at a metal-dielectric interface with an epsilon-near-zero transition layer" by Kevin Roccapriore et al., Physical Review B 103, L161404 (2021).