In mathematics, Abel's theorem for power series relates a limit of a power series to the sum of its coefficients. It is named after Norwegian mathematician Niels Henrik Abel, who proved it in 1826.^[1]

Theorem

Let the Taylor series

$${\displaystyle G(x)=\sum _{k=0}^{\infty }a_{k}x^{k}}$$

be a power series with real coefficients ${\displaystyle a_{k}}$ with radius of convergence ${\displaystyle 1.}$ Suppose that the series

$${\displaystyle \sum _{k=0}^{\infty }a_{k}}$$

converges. Then ${\displaystyle G(x)}$ is continuous from the left at ${\displaystyle x=1,}$ that is,

$${\displaystyle \lim _{x\to 1^{-}}G(x)=\sum _{k=0}^{\infty }a_{k}.}$$

The same theorem holds for complex power series

$${\displaystyle G(z)=\sum _{k=0}^{\infty }a_{k}z^{k},}$$

provided that ${\displaystyle z\to 1}$ entirely within a single Stolz sector, that is, a region of the open unit disk where

$${\displaystyle |1-z|\leq M(1-|z|)}$$

for some fixed finite ${\displaystyle M>1}$. Without this restriction, the limit may fail to exist: for example, the power series

$${\displaystyle \sum _{n>0}{\frac {z^{3^{n}}-z^{2\cdot 3^{n}}}{n}}}$$

converges to ${\displaystyle 0}$ at ${\displaystyle z=1,}$ but is unbounded near any point of the form ${\displaystyle e^{\pi i/3^{n}},}$ so the value at ${\displaystyle z=1}$ is not the limit as ${\displaystyle z}$ tends to 1 in the whole open disk.

Note that ${\displaystyle G(z)}$ is continuous on the real closed interval ${\displaystyle [0,t]}$ for ${\displaystyle t<1,}$ by virtue of the uniform convergence of the series on compact subsets of the disk of convergence. Abel's theorem allows us to say more, namely that ${\displaystyle G(z)}$ is continuous on ${\displaystyle [0,1].}$

Stolz sector

20 Stolz sectors, for ${\displaystyle M}$ ranging from 1.01 to 10. The red lines are the tangents to the cone at the right end.

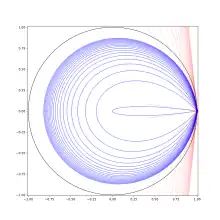
The Stolz sector ${\displaystyle |1-z|\leq M(1-|z|)}$ has explicit equation

$${\displaystyle y^{2}=-{\frac {M^{4}(x^{2}-1)-2M^{2}((x-1)x+1)+2{\sqrt {M^{4}(-2M^{2}(x-1)+2x-1)}}+(x-1)^{2}}{(M^{2}-1)^{2}}}}$$

and is plotted on the right for various values.

The left end of the sector is ${\displaystyle x={\frac {1-M}{1+M}}}$, and the right end is ${\displaystyle x=1}$. On the right end, it becomes a cone with angle ${\displaystyle 2\theta }$ where ${\displaystyle \cos \theta ={\frac {1}{M}}}$.

Remarks

As an immediate consequence of this theorem, if ${\displaystyle z}$ is any nonzero complex number for which the series

$${\displaystyle \sum _{k=0}^{\infty }a_{k}z^{k}}$$

converges, then it follows that

$${\displaystyle \lim _{t\to 1^{-}}G(tz)=\sum _{k=0}^{\infty }a_{k}z^{k}}$$

in which the limit is taken from below.

The theorem can also be generalized to account for sums which diverge to infinity. If

$${\displaystyle \sum _{k=0}^{\infty }a_{k}=\infty }$$

then

$${\displaystyle \lim _{z\to 1^{-}}G(z)\to \infty .}$$

However, if the series is only known to be divergent, but for reasons other than diverging to infinity, then the claim of the theorem may fail: take, for example, the power series for

$${\displaystyle {\frac {1}{1+z}}.}$$

At ${\displaystyle z=-1}$ the series is equal to ${\displaystyle 1-1+1-1+\cdots ,}$ but ${\displaystyle {\tfrac {1}{1+1}}={\tfrac {1}{2}}.}$

We also remark the theorem holds for radii of convergence other than ${\displaystyle R=1}$: let

$${\displaystyle G(x)=\sum _{k=0}^{\infty }a_{k}x^{k}}$$

be a power series with radius of convergence ${\displaystyle R,}$ and suppose the series converges at ${\displaystyle x=R.}$ Then ${\displaystyle G(x)}$ is continuous from the left at ${\displaystyle x=R,}$ that is,

$${\displaystyle \lim _{x\to R^{-}}G(x)=G(R).}$$

Applications

The utility of Abel's theorem is that it allows us to find the limit of a power series as its argument (that is, ${\displaystyle z}$) approaches ${\displaystyle 1}$ from below, even in cases where the radius of convergence, ${\displaystyle R,}$ of the power series is equal to ${\displaystyle 1}$ and we cannot be sure whether the limit should be finite or not. See for example, the binomial series. Abel's theorem allows us to evaluate many series in closed form. For example, when

$${\displaystyle a_{k}={\frac {(-1)^{k}}{k+1}},}$$

we obtain

$${\displaystyle G_{a}(z)={\frac {\ln(1+z)}{z}},\qquad 0<z<1,}$$

by integrating the uniformly convergent geometric power series term by term on ${\displaystyle [-z,0]}$; thus the series

$${\displaystyle \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k+1}}}$$

converges to ${\displaystyle \ln 2}$ by Abel's theorem. Similarly,

$${\displaystyle \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2k+1}}}$$

converges to ${\displaystyle \arctan 1={\tfrac {\pi }{4}}.}$

${\displaystyle G_{a}(z)}$ is called the generating function of the sequence ${\displaystyle a.}$ Abel's theorem is frequently useful in dealing with generating functions of real-valued and non-negative sequences, such as probability-generating functions. In particular, it is useful in the theory of Galton–Watson processes.

Outline of proof

After subtracting a constant from ${\displaystyle a_{0},}$ we may assume that ${\displaystyle \sum _{k=0}^{\infty }a_{k}=0.}$ Let ${\displaystyle s_{n}=\sum _{k=0}^{n}a_{k}\!.}$ Then substituting ${\displaystyle a_{k}=s_{k}-s_{k-1}}$ and performing a simple manipulation of the series (summation by parts) results in

$${\displaystyle G_{a}(z)=(1-z)\sum _{k=0}^{\infty }s_{k}z^{k}.}$$

Given ${\displaystyle \varepsilon >0,}$ pick ${\displaystyle n}$ large enough so that ${\displaystyle |s_{k}|<\varepsilon }$ for all ${\displaystyle k\geq n}$ and note that

$${\displaystyle \left|(1-z)\sum _{k=n}^{\infty }s_{k}z^{k}\right|\leq \varepsilon |1-z|\sum _{k=n}^{\infty }|z|^{k}=\varepsilon |1-z|{\frac {|z|^{n}}{1-|z|}}<\varepsilon M}$$

when ${\displaystyle z}$ lies within the given Stolz angle. Whenever ${\displaystyle z}$ is sufficiently close to ${\displaystyle 1}$ we have

$${\displaystyle \left|(1-z)\sum _{k=0}^{n-1}s_{k}z^{k}\right|<\varepsilon ,}$$

so that ${\displaystyle \left|G_{a}(z)\right|<(M+1)\varepsilon }$ when ${\displaystyle z}$ is both sufficiently close to ${\displaystyle 1}$ and within the Stolz angle.

Related concepts

Converses to a theorem like Abel's are called Tauberian theorems: There is no exact converse, but results conditional on some hypothesis. The field of divergent series, and their summation methods, contains many theorems of abelian type and of tauberian type.

See also

• Abel's summation formula – Integration by parts version of Abel's method for summation by parts
• Nachbin resummation – Theorem bounding the growth rate of analytic functionsPages displaying short descriptions of redirect targets
• Summation by parts – Theorem to simplify sums of products of sequences

Further reading

• Ahlfors, Lars Valerian (September 1, 1980). Complex Analysis (Third ed.). McGraw Hill Higher Education. pp. 41–42. ISBN 0-07-085008-9. - Ahlfors called it Abel's limit theorem.

References

External links

• Abel summability at PlanetMath. (a more general look at Abelian theorems of this type)
• A.A. Zakharov (2001) [1994], "Abel summation method", Encyclopedia of Mathematics, EMS Press
• Weisstein, Eric W. "Abel's Convergence Theorem". MathWorld.